Missing square puzzle
The missing square puzzle is an optical illusion used in mathematics classes to help students reason about geometrical figures. It depicts two arrangements of shapes, each of which apparently forms a 13×5 right-angled triangle, but one of which has a 1×1 hole in it.
Contents |
Solution
The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, because what would be the hypotenuse is bent. In other words, the hypotenuse does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13 × 5 triangle cannot be created from the given component parts.
The four figures (the yellow, red, blue and green shapes) total 32 units of area, but the triangles are 13 wide and 5 tall, so it seems, that the area should be 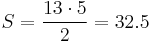 units. But the blue triangle has a ratio of 5:2 (=2.5:1), while the red triangle has the ratio 8:3 (≈2.667:1), and these are not the same ratio. So the apparent combined hypotenuse in each figure is actually bent.
units. But the blue triangle has a ratio of 5:2 (=2.5:1), while the red triangle has the ratio 8:3 (≈2.667:1), and these are not the same ratio. So the apparent combined hypotenuse in each figure is actually bent.
The amount of bending is around 1/28th of a unit (1.245364267°), which is difficult to see on the diagram of this puzzle. Note the grid point where the red and blue hypotenuses mate, and compare it to the same point on the other figure; the edge is slightly over or under the mark. Overlaying the hypotenuses from both figures results in a very thin parallelogram with the area of exactly one grid square, the same area "missing" from the second figure.
According to Martin Gardner,[1] the puzzle was invented by a New York City amateur magician Paul Curry in 1953. The principle of a dissection paradox has however been known since the 1860s.
The integer dimensions of the parts of the puzzle (2, 3, 5, 8, 13) are successive Fibonacci numbers. Many other geometric dissection puzzles are based on a few simple properties of the famous Fibonacci sequence.[2]
Similar puzzles
A different puzzle of the same kind (depicted in the animation) uses four equal quadrilaterals and a small square, which form a larger square. When the quadrilaterals are rotated about their centers they fill the space of the small square, although the total area of the figure seems unchanged. The apparent paradox is explained by the fact that the side of the new large square is a little smaller than the original one. If  is the side of the large square and
is the side of the large square and  is the angle between two opposing sides in each quadrilateral, then the quotient between the two areas is given by
is the angle between two opposing sides in each quadrilateral, then the quotient between the two areas is given by 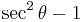 . For θ = 5°, this is approximately 1.00765, which corresponds to a difference of about 0.8%.
. For θ = 5°, this is approximately 1.00765, which corresponds to a difference of about 0.8%.
References
- ^ Martin, Gardner (1956). Mathematics Magic and Mystery. Dover. pp. 139–150.
- ^ Weisstein, Eric. "Cassini's Identity". http://mathworld.wolfram.com/CassinisIdentity.html.
External links
- A printable Missing Square variant with a video demonstration.
- Curry's Paradox: How Is It Possible? at cut-the-knot
- Triangles and Paradoxes at archimedes-lab.org
- The Triangle Problem or What's Wrong with the Obvious Truth
- Jigsaw Paradox
- The Eleven Holes Puzzle
- Very nice animated Excel workbook of the Missing Square Puzzle
- A video explaining Curry's Paradox and Area by James Stanton